ECDSA及加速方法介绍

公钥密码学(Public-key cryptography)

公开密钥密码学也称非对称式密码学，是密码学的一种算法，它需要两个密钥，一个是公开密钥，另一个是私有密钥；公钥用作加密，私钥则用作解密。使用公钥把明文加密后所得的密文，只能用相对应的私钥才能解密并得到原本的明文。

基于公开密钥加密的特性，它还能提供数字签名的功能，使电子文件可以得到如同在纸本文件上亲笔签署的效果。

公钥密码学的两个最著名的应用是公钥加密和数字签名。

公钥加密

公钥加密指的是由对应的一对唯一性密钥（即公开密钥和私有密钥）组成的加密方法。

常见算法

RSA、ECC、Diffie-Helmlan、ElGamal等等

数字签名

数字签名是一种功能类似写在纸上的普通签名、但是使用了公钥加密领域的技术，以用于鉴别数字信息的方法。什么是数字签名？

数字签名算法(DSA)

RSA

RSA是目前计算机密码学中最经典算法，也是目前为止使用最广泛的数字签名算法。RSA数字签名算法主要包括MD和SHA两种算法。

DSA算法

和RSA不同之处在于它不能用作加密和解密，也不能进行密钥交换，只用于签名，所以它比RSA要快很多，其安全性与RSA相比差不多。DSA的一个重要特点是两个素数公开，这样，当使用别人的p和q时，即使不知道私钥，你也能确认它们是否是随机产生的，还是作了手脚。RSA算法却做不到。

ECDSA

ECC与DSA的结合。相同密钥长度下，安全性能更高。计算量小，处理速度快，在私钥的处理速度上（解密和签名），ECC远 比RSA、DSA快得多。存储空间占用小，且带宽要求低。

EdDSA

在ECDSA上进行了优化，使用了爱德华曲线。签名过程中不需要唯一的随机数,能够避免随机数引发的安全问题。公钥和签名值都较小，计算更完备。

上文主要介绍了一些密码学的常识，后面主要介绍论文Elliptic Curve Cryptography with Efficiently Computable Endomorphisms and Its Hardware Implementations for the Internet of Things中的内容，即ECDSA和涉及到的证书验证计算优化。

ECDSA(椭圆曲线数字签名算法)

ECDSA(Elliptic Curve Digital Signature Algorithm)中文介绍&wiki

In cryptography, the Elliptic Curve Digital Signature Algorithm (ECDSA) offers a variant of the Digital Signature Algorithm (DSA) which uses elliptic curve cryptography.

ECDSA使用椭圆曲线密码学进行数字签名。

ECDSA方程

Weierstrass曲线形式：

$$E_s: y^2=(x^3+ax+b)\mod\ p$$

曲线关于X轴对称

参数

为曲线参数

为曲线上面点的个数

为曲线上一点

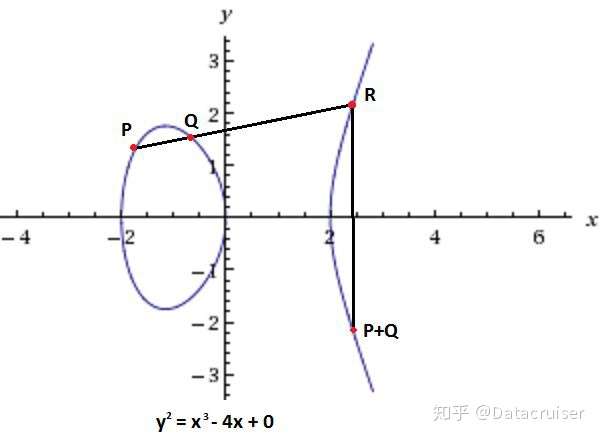
点的加法与乘法

将一个点和另外一个点相加将得到点，如果我们从到 画一条线，并延长与曲线相交于第三个点，则为 的负值，别忘记曲线是关于轴对称的。在这种情况下，我们定义来表示在 轴上面的对称点。具体可以看下面这张图。

如果和重合，做切线。

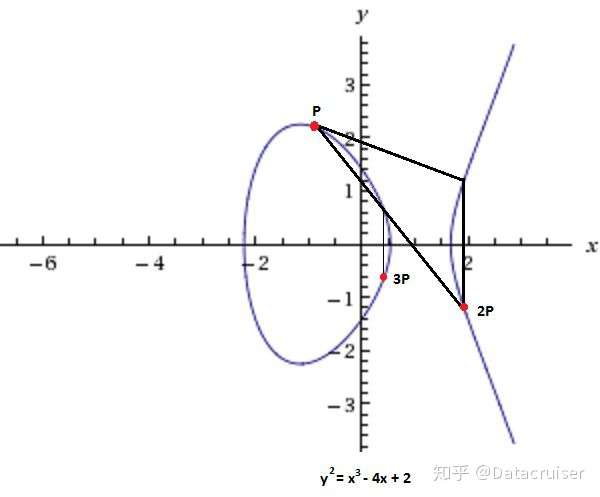
同样的机制，如果你进行，其结果为经过的切线与曲线的交点关于轴的对称点，然后可以看作是点与 点相加的结果。这就可以用来对椭圆曲线点乘法进行定义：就是点自身进行次相加，以下图为例。

私钥与公钥

私钥是一个随机数，公钥是将曲线上的点与私钥相乘以后得到的曲线上的点。其中是曲线上面的参考点。

1.随机私钥

2.公钥，一个点

生成签名

1.产生随机数

2.计算

3.为点的坐标

4.整数 如SHA-1

5., 为的模的乘法逆元

签名内容，两个数值

签名验证

计算上述点，若点的坐标与相等，则签名有效

安全性

需要同时知道随机数和私钥才能够计算出，但是需要和公钥来对签名进行确认和验证。并且由于以及再加上离散对数问题的困难性，没有办法找到私钥，也就无法在不知道私钥的情况下伪造签名。

有一个点，知道和，但无法据此求出。

文章关注问题

ECDSA的一个重要问题是，验证过程非常耗时。

在ECDSA签名验证时，需要计算一个双标量乘法——，其中是椭圆上一点，生成了素数阶为的组，是组中任意的一个元素，和是范围为的两个整数。

的计算会比较耗时，尤其对于那些资源受限的iot设备。本文研究了包含有效自同态的扭曲爱德华曲线上的计算，能够减少50%的点乘次数，以加速双标量乘法的运算。此外，本文还设计了实现该操作的两个硬件结构。一是0.13 mm CMOS ASIC中的小型处理器。二是使用FPGA加速的快速证书验证，可以用于应用的服务器端。

文献中涉及的一些算法内容：

GLV方法(使用自同态)

为椭圆曲线，有限域

素数阶为

假设存在一个计算高效的自同态，

对于特殊的曲线，是已知的，且可以通过一些特性快速计算

可以将的计算变为的形式，其中&只有原来长度的一半左右。这两个标量乘法可以通过Shamir’s trick同时计算。

本文的样例曲线

本文通过CM判别式和一些性能因素，选择了曲线

$$E_{-1,1}/F_p:-x^2+y^2=1+x^2y^2$$

有一个高效的自同态

$$\phi_t(x,y)=(\alpha\cdot x,1/y)$$

中

计算双标量乘法的加速方法(*)

目标：计算出，同时降低计算时间（得到具体表达式后的计算时间，也可以用点加点乘的次数表示）和空间（主要指事先计算的内容量）

两个单标量乘法

最简单直接的方法，分别计算两个标量乘法

其中计算比较简单，是固定且提前知道的，可以通过fixed-base comb method[12,algorithm3.44]计算

由于是固定的，所以我们可以花更多时间在事先计算上，以使得验证时计算的时间更短

是的长度，是window的宽度，，将分为个比特串，每个串的长度都为

表示为

$$k=k^{w-1}||\cdots||k^1||k^0$$

为了加速计算，点

$$[a_{w-1},\cdots,a_2,a_1,a_0]P=a_{w-1}2^{(w-1)d}P+\cdots+a_22^{2d}P+a_12^dP+a_0P$$

对于所有可能的比特串都要事先计算好。届时根据实际的值以及分为个比特串后分别的值，在事先计算好的点集中寻找对应点。

第二部分的计算使用到了binary method(类似快速幂)

由于可能是群内的任意点，所以无法进行事先计算

Interleaving Method

Shamir’s trick：给定宽度，计算出对于所有的

在个步骤中每一步，累加器乘上再加上，window中和值对应在表中（事先计算好得到的一个表）的的值

特别地，本文中的Interleaving Method是将固定为1，所以方法简化为

首先计算出

然后从低位开始一位一位搜索比特，如果，，那么对应该位，如果 ，，对应该位,如果，对应该位

Joint Sparse Form

与上面的方法相似，不同的是，该JSF方法先将和用带符号的二进制表示，以最小化joint Hamming weight。JSF表达形式与前面的表示方式类似，优势在于全为0的列（也就是该位上的）数量更多。

需要提前计算&，因此提前计算量会比Interleaving Method大。

Window Method

在Shamir’s trick中提到的方法，更类似于一个划分方法，一般是与其他方法结合使用(alg3.44中的window)。本文中，Interleaving Method和Joint Sparse Form都可以看做是window宽度为1的方法。

Double Scalar Multiplication with Endomorphism

本文主要研究的方法。结合了自同态，查表，交叉计算的方法（还可以结合window的方法，但理论分析后结合window方法不如不结合的方法）

Algorithm3.74是一个用于分解为使得 and

然后通过Montgomery’s trick计算点&（由于曲线和其自同态的特殊性，该计算非常快捷）

生成15个点的查找表，该表包括、、、的所有组合形式

最后以交叉的形式计算

具体就是写成二进制形式，从高到低遍历每一位，然后累加器先乘2，再根据该位(可以看做是window框柱的一列)中4个元素的该位值，在表中查找相应的点，累加器加上该点。

上述方法表现比较

考虑到本文研究的场景主要是为资源受限的iot设备涉及加速方法，所以根据表现和RAM需求，方法(d)是最适合用于加速双标量乘法的方法。

Guide Elliptic Curve Cryptography